Smooth Minimum

What is Smooth Min?

It is common to apply the min operator to create unions of objects when raymarching distance fields. This is a CSG operation implemented in a single line of code, which is a major advantage.

\[\text{min}(a,b) = \begin{cases} a, &\text{if } a < b\\ b, &\text{otherwise}\end{cases}\]

The min operator is a \(C^0\) function, which means its derivative is not continuous. This is a downside when trying to model organic objects, as can be seen in the following images.

Union of a sphere and a set of cones using min and smooth min

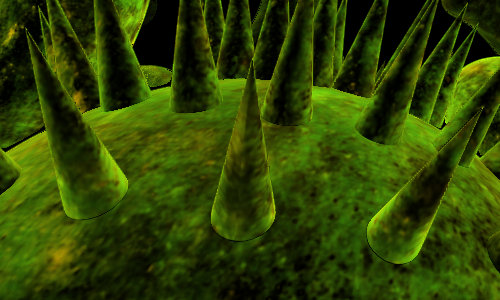
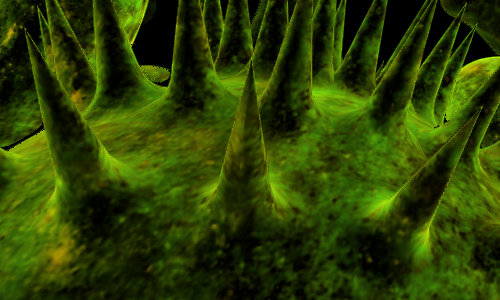
Inigo Quilez (iq) proposed an operator called polynomial smooth minimum that is widely used in Shadertoy. It employs linear interpolation to blend the two input distance fields. I have used the below code in some of my shaders but never had the time to fully comprehend it, so I decided to derive it myself.

// Polynomial smooth minimum by iq
float smin(float a, float b, float k) {
  float h = clamp(0.5 + 0.5*(a-b)/k, 0.0, 1.0);
  return mix(a, b, h) - k*h*(1.0-h);
}

Derivation of the Polynomial Smooth Minimum

The idea is really simple: we should smoothly interpolate the values \(a\) and \(b\) if they are near each other, otherwise we return the true maximum. Formally, we define these values to be close if \(a-b \in (\text{-}k,k)\), in which \(k\) controls the interpolation range. Therefore, our smooth approximation to min should be of the form

\[\begin{equation} \text{smin}(a, b, k) = \begin{cases} a, &\text{if } a - b \geq k \\ b, &\text{if } a - b \leq \text{-}k \\ f(a, b, k), &\text{if } a - b \in (\text{-}k, k) \end{cases}, \end{equation}\]

where \(f(a,b,k)\) is a smooth interpolator. We also want it to be at least \(C^1\) so that it is visually smooth for our shaders. A first guess for this function would be linear interpolation

\[\begin{equation} f(a,b,k) = a + h(b-a) \quad h \in [0,1], \end{equation}\]

in which we compute \(h\) based on the input values \(a\) and \(b\) by remapping the interval \([-k, k]\) to \([0, 1]\) as such that

\[\begin{equation} h = \frac{1}{2} + \frac{(a - b)}{2k}. \label{eq:h} \end{equation}\]

By plotting smin applied to functions \(a = \sin x\) and \(b = e^{-x}\) we can notice that it is a reasonable approximation of min for small values of \(k\).

Smooth min approximates min for k = 0.01 but is incorrect for k = 0.8

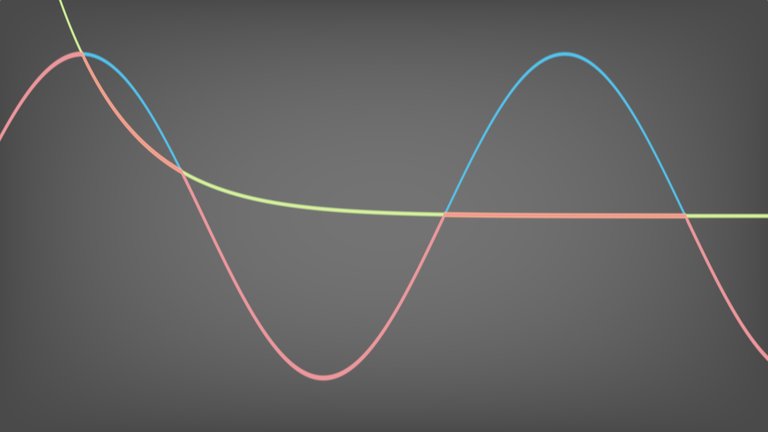
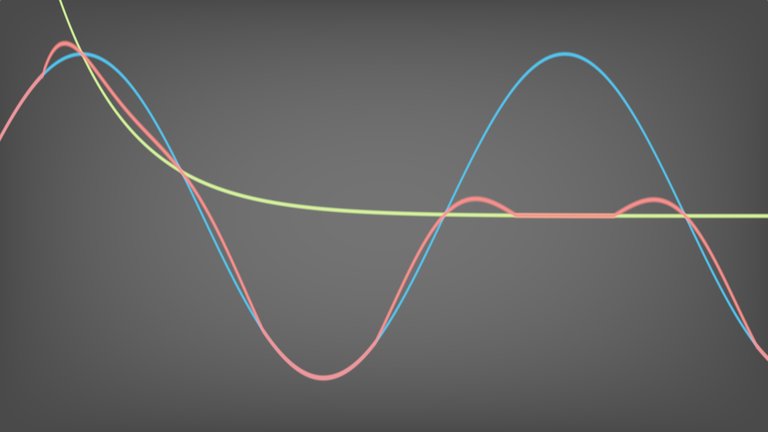
The error occurs because of discontinuities in the derivative of \(f(a, b, k)\) with respect to \(x\), which is given by

\[\begin{equation} \frac{df}{dx} = \frac{da}{dx} + \frac{dh}{dx}(b - a) + h\left(\frac{db}{dx} - \frac{da}{dx}\right). \tag{1} \label{eq:derivative} \end{equation}\]

Let us analyze what happens at the boundaries of \((\text{-}k, k)\). If \(a-b=-k\) then \(h = 0\) and the above equation reduces to

\[\begin{equation} \frac{df}{dx} = \frac{da}{dx} + k\frac{dh}{dx}. \tag{2} \label{eq:reduce-1} \end{equation}\]

Otherwise, if \(a-b=k\) then \(h = 1\) and we have

\[\begin{equation} \frac{df}{dx} = \frac{db}{dx} - k\frac{dh}{dx}. \tag{3} \label{eq:reduce-2} \end{equation}\]

We respectively want equations (\(\ref{eq:reduce-1}\)) and (\(\ref{eq:reduce-2}\)) to be \(\frac{da}{dx}\) and \(\frac{db}{dx}\), so that the derivative of \(f(a, b, k)\) matches the ones for \(a\) and \(b\) at the limits of interval \([\text{-}k, k]\). In other words, we want to get rid of the second term in each of these equations.

We can start by adding \(-k\frac{dh}{dx}\) into the right-hand side of \((\ref{eq:derivative})\) so as to cancel out the second term in \((\ref{eq:reduce-1})\). However, this changes the second term of \((\ref{eq:reduce-2})\) to be \(-2k\frac{dh}{dx}\). Hence, we need to add \(2kh\frac{dh}{dx}\) into the right-hand side of \((\ref{eq:derivative})\). This new term is zero in \((\ref{eq:reduce-1})\) because \(h=0\) in the former, and it cancels out the prior \(-2k\frac{dh}{dx}\) in \((\ref{eq:reduce-2})\) as \(h=1\) in the latter. Therefore, the corrected derivative of \(f(a,b,k)\) must be

\[\frac{df}{dx} = \frac{da}{dx} + \frac{dh}{dx}(b - a) + h\left(\frac{db}{dx} - \frac{da}{dx}\right) - k\frac{dh}{dx} + 2kh\frac{dh}{dx}.\]

By integrating the above equation, rearranging its terms, and using GLSL notation, we can conclude that

\[\begin{align} f(a, b, k) &= a + h(b - a) - kh + kh^2 \\ &= a(1-h) + hb - kh(1 - h) \\ &= \text{mix}(a, b, h) - kh(1 - h). \end{align}\]

There is probably a simpler way around this derivation. Nevertheless, I think this exercise has been really interesting to me, and I hope for you as well. Thank you for reading!

Update: At the time this post was published, Inigo Quilez had provided the operator without explaining it. You can now read his own description.