Bacterium

Bacterium was my first shader of the week at Shadertoy in May 2015. This post describes a breakdown of the effect.

Modeling the Bacteria

The bacteria are distorted capsules that squiggle and rotate as a function of position and time. Their distance field is a modified version of iq’s capsule/line function that uses modular arithmetic to achieve repetition. The squiggling was done by slightly rotating the space around their local origin.

float capsules(vec3 p) {
  vec3 q - floor(p/4.0); // position repeated through space (used for rotating around)
  p = mod(p, 4.0) - 2.0; // modular arithmetic to repeat the capsules

  // rotational movement around the capsule's local frame
  // this keeps all bacteria rotating around endlessly
  p.yz = p.yz*cos(iGlobalTime + q.z) + vec2(-p.z, p.y)*sin(iGlobalTime + q.z);
  p.xy = p.xy*cos(iGlobalTime + q.x) + vec2(-p.y, p.x)*sin(iGlobalTime + q.x);
  p.zx = p.zx*cos(iGlobalTime + q.y) + vec2(-p.x, p.z)*sin(iGlobalTime + q.y);

  // squiggle on the Y axis (it's small rotation around Z as a function of X)
  float angle = .3*cos(iGlobalTime)*p.x;
  p.xy = cos(angle)*p.xy + sin(angle)*vec2(-p.y, p.x); p.x += 1.0;

  // distance to capsule/line adapted from iq's function
  float k = clamp(2.0*p.x/4.0, 0.0, 1.0); p.x -= 2.*k;
  return length(p) - .5;
}

The bacteria are simple capsules. Squiggles are created by rotating the space around the local origin.

At a first glance, the overall motion of the bacteria may seem a little bit random. But that’s just an effect of the combined motion of the camera and their squiggling. Essentially, the difference in phase of each capsule is just a constant offset, and you can easily spot that in the shader if you pay attention.

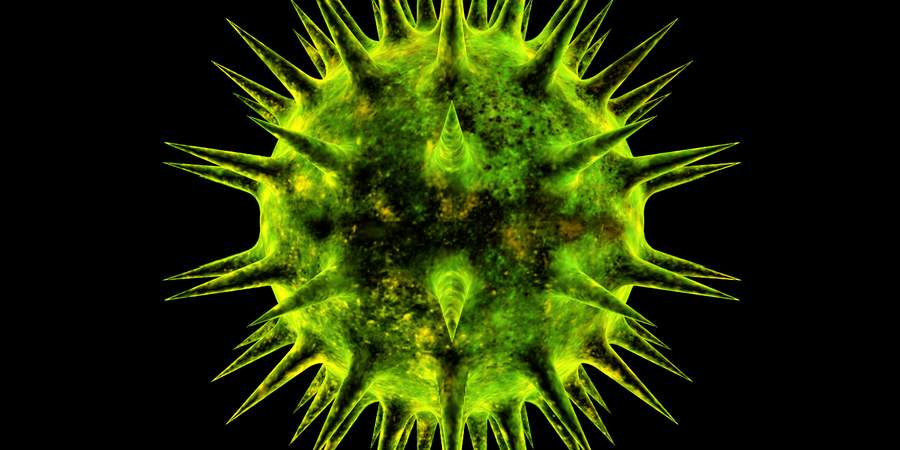
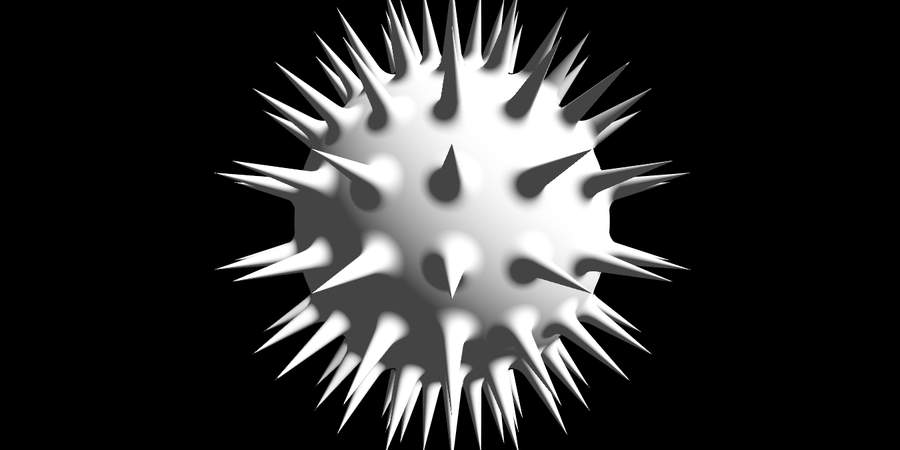
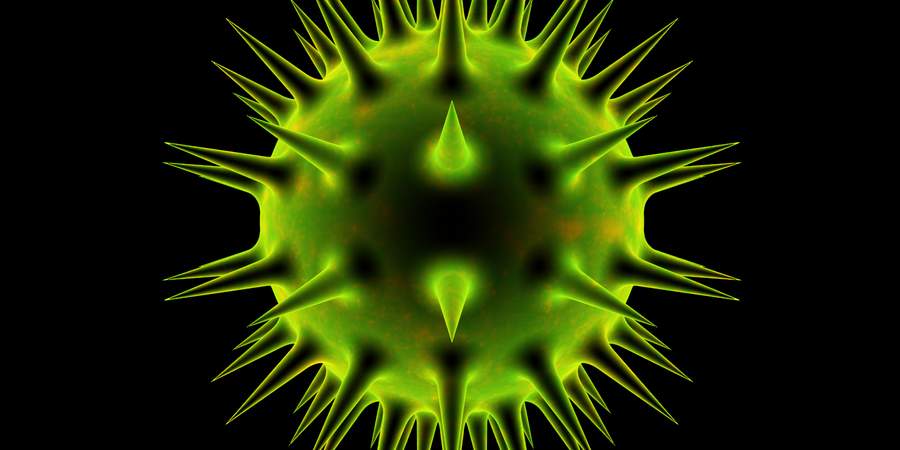
Modeling the Viruses

The viruses are just spheres with attached cones. They are a good example of how simple shapes can become an interesting object when joined together. I applied modular arithmetic in polar coordinates to radially repeat the cones and blended them with the sphere using iq’s smooth minimum.

// Modular repetition in polar coordinates
vec2 rep(vec2 p) {
    // transform into polar coordinates
    float a = atan(p.y, p.x); 
	
    // modular repetition
    a = mod(a, 2.0*PI/18.) - PI/18.; 
	
    // transform back into euclidean coordinates
    return length(p)*vec2(cos(a), sin(a)); 
}

float spikedBall(vec3 p) {
    float d = length(p) - 1.2; // distance to a sphere
        
    p.xz = rep(p.xz); // angular repetition on the XZ plane    
    p.xy = rep(p.xy); // angular repetition on the XY plane

    // returns the smoothed-minimun distance 
    // between the sphere and the spikes
    return smin(d, length(p.yz)-.1+abs(.15*(p.x-1.0)), 0.1); 
}

A single cone is repeated in a radial manner to model the spikes on the virus.

Lighting and Shading

I started by applying on the models a cube map that is one of the default textures in Shadertoy. But instead of using the sample as an albedo value, I made it an interpolation factor between a green and a yellow color. The result was modulated by the contribution of a simple rim light model.

Albedo values and the rim light model used for shading

Modulating the albedo by the rim light model

For conclusion, I thought the model still needed some details and decided to include a bump map. Both my cubeMap and bumpMap methods were based on some of iq’s shaders.

vec3 shade(vec3 ro, vec3 rd, float t) {
    vec3 p = ro + t*rd, // computes the hit point of the ray
    vec3 n = normal(p); // computes the normal vector at the hit point

    const vec3 green = pow(vec3(93,202,49)/255., vec3(2.2));
    const vec3 yellow = pow(vec3(255,204,0)/255., vec3(2.2));
    
	// accesses the cube map as a single-channel texture
    float k = cubeMap(.5*p, n); 
    n = bumpMap(.5*p, n, k);

	// modulates the color according to a rim light model
    vec3 col = mix(green, yellow, k)*(1.0-dot(-rd,n));
        
    return col*exp(-.008*t*t); // applies fog.
}

Final shading result when using bump mapping